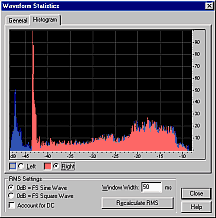
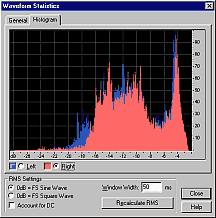
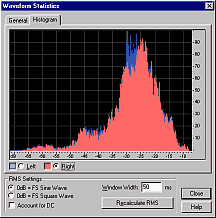



Having calculated RMS signal levels every 50ms through the file, a single value must be calculated to represent the perceived loudness of the entire file. The above histograms show how many times each RMS value occurred in each file.
The most common RMS value in the speech track was -45dB (background noise) - so the most common RMS value is clearly NOT a good indicator of perceived loudness! The average RMS value is similarly misleading with the speech sample, and also with classical music.
A good method to determine the overall perceived loudness is to sort the RMS energy values into numerical order, and then pick a value near the top of the list.
How far down the sorted list should we look for a representative value? I tried values from 70% to 95%. For highly compressed pop music (e.g. the middle graph above, where there are many values near the top), the choice makes little difference. For speech and classical music, the choice makes a huge difference. The value which most accurately matches human perception of perceived loudness is around 95%, so this value is used by Replay Level.
Since MATLAB has a dedicated sort function, and simple indexing into arrays, this task is carried out in two lines of code (from ReplayGain.m):
% Sort the Vrms values into numerical order
Vrms_all=sort(Vrms_all);
% Pick the 95% value
Vrms=Vrms_all(round(length(Vrms_all)*0.95));
...where length(Vrms_all)*0.95 is just an index 95% of the way into the sorted array. It must be "round"ed because MATLAB will not accept non-integer array indexing.
Someone, PLEASE, tell me the name of the statistical process of sorting data and picking the value a certain fraction along the list! Thank you.
The value of 95% may be altered if a better value is found, but it seems to work well.